บทที่ 7.ทฤษฎีเมตริกซ์

เมทริกซ์ หมายถึง กลุ่มของจำนวนจริงที่นำมาจัดเรียนงกันให้เป็นแถว แต่ละแถวมมีจำนวนที่เท่าๆกัน โดยมีวงเล็บเล็ก ( ) หรือวง เลบ็บ [ ] ปิดล้อมไว้ เช่น โดยทั่วไปแล้วเรามักนิยมใช้อักษร A , B , C , ... แทนเมทริกซ์ และใช้ตัวอักษรพิมพ์เล็ก a , b , c , ... แทนสมาชิกของเมทริกซ์ แต่ถ้าสมาชิกของเมทริกซ์มีจำนวนมาก เราจะใช้อักษรเพียงตัวเดียวแทนสมาชิกและเขียนจำนวนต่อท้ายตัวอักษรดังกล่าวเพื่อบอกตำแหน่ง ในระดับที่ต่ำลงไปเล็กน้อย  เช่น     จำนวนที่เขียนตามหลังตัวอักษรนั้นจำทำหน้าที่บ่งบอกถึงตำแหน่งของสมาชิก เช่น เป็นสมาชิกในตำแหน่ง แถวที่ 1 หลักที่ 1     เป็นสมาชิกในตำแหน่ง แถวที่ 3 หลักที่ 1   เป็นสมาชิกในตำแหน่ง แถวที่ 3 หลักที่ 3 สรุปหมายถึง สมาชิกในตำแหน่ง แถวที่ i หลักที่ j  พูดกันแบบง่ายก็คือ ตัวเลขตัวหน้า คือ แถว ตัวหลัง คือ หลัก นั่นเอง      ถ้าเมทริกซ์ A เป็นเมทริกซ์มิติเราสามารถเขียนสัญลักษณ์แทนเมทริกซ์ A ได้ดังนี้         แต่ในการเขียนเช่นนี้ค่อนข้างยืดยาว เราจึงนิยมใช้เขียนเป็น                                                                                                         แทน โดยที่ i (แถว) = 1 , 2 , 3 , .... , m                                                    j (หลัก) = 1 , 2 , 3 , .... , n         หรืออาจจะเขียนให้สั้นกว่านี้ได้อีกดังนี้ดังนั้น ถ้านักเรียนเห็นสัญลักษณ์นี้ ต้องทราบทันที่ว่า เมทริกซ์ A มีมิติ และมีเป็นตัวแทนของสมาชิกโดยทั่วไป        ตัวอย่าง ถ้า  แสดงว่า เมทริกซ์ A มี 2 แถว 2 หลัก            ดังนั้น   แต่ละจำนวนที่ประกอบขึ้นเป็นเมทริกซ์เรียกว่า สมาชิก (Elements) ของเมทริกซ์ กำหนดให้ a เป็นเมทริกซ์ใดๆ ตำแหน่งสมาชิกของเมทริกซ์ a

มิต ถ้าเมทริกซ์  M1M1  มีสมาชิก mm แถว  และ nn หลัก เราเรียกเมทริกซ์นั้นว่า เมทริกซ์ M1M1 มีมิติ m×nm×n หรือเรียกว่า  เมทริกซ์ M1M1 มีขนาด m×nm×n พิจารณาเมทริกซ์ M1,M2,M3M1,M2,M3 จากตัวอย่างข้างบนเราจะได้ เมทริกซ์ M1M1  มีมิติ 2×32×3 เมทริกซ์ M2M2  มีมิติ 3×23×2 เมทริกซ์ M3M3  มีมิติ 2×22×2

แถวและคอลัมน์

เมทริกซ์ คือกลุ่มของจำนวนหรือสมาชิกของริงใดๆ เขียนเรียงกันเป็นรูปสี่เหลี่ยมผืนผ้าหรือจัตุรัส กล่าวคือเรียงเป็นแถวในแนวนอน และเรียงเป็นคอลัมน์ในแนวตั้ง เรามักเขียนเมทริกซ์เป็นตารางที่ไม่มีเส้นแบ่งและเขียนวงเล็บคร่อมตารางไว้ (ไม่ว่าจะเป็นวงเล็บโค้งหรือวงเล็บเหลี่ยม) เช่น               เราเรียกแถวในแนวนอนของเมทริกซ์ว่า แถว เรียกคอลัมน์ในแนวตั้งของเมทริกซ์ว่า หลัก และเรียกจำนวนแต่ละจำนวนเในเมทริกซ์ว่า สมาชิก ของเมทริกซ์ การกล่าวถึงสมาชิกของเมทริกซ์ จะต้องระบุตำแหน่งให้ถูกต้อง เช่น จากตัวอย่างข้างบน สมาชิกที่อยู่ในแถวที่ 2 หลักที่ 3 คือเลข 4 สมาชิกที่อยู่ในแถวที่ 2 หลักที่ 2 คือเลข 15 สมาชิกที่อยู่ในแถวที่ 3 หลักที่ 1 คือเลข 5

ชนิดของเมตริกซ์

1.เมทริกซ์ที่มีเพียงแถวเดียว เราจะเรียกว่า เมทริกซ์แถว หรือ row matrix นะคะ ตัวอย่างเช่น  ,  เป็นต้น 2.ส่วนเมทริกซ์ที่มีเพียงหลักเดียว เราเรียกว่า เมทริกซ์หลัก หรือ column matrix นั่นเอง เช่น ,  3.แต่ถ้าสมาชิกทุกตัวของเมทริกซ์เป็นศูนย์หมด เราเรียกว่า เมทริกซ์ศูนย์ หรือ zero matrix แทนด้วยสัญลักษณ์เช่น ,  4.เมทริกซ์ที่มีจำนวนแถวและจำนวนหลักเท่ากัน นั่นคือ เป็นเมทริกซ์มิติ เราเรียกเมทริกซ์ที่มีลักษณะนี้ว่า เมทริกซ์จัตุรัส หรือ squarematrix ตัวอย่าง เช่น  เมทริกซ์จัตุรัส จะมีสมาชิกที่อยู่ในแนวเส้นทแยงมุม 2 ลักษณะ คือ ทแยงมุมจากซ้ายบนลงมาขวาล่าง กับ ทแยงมุมจากซ้ายล่างขึ้นไปขวาบน แต่เราจะกล่าวถึง คือ สมาชิกในแนวเส้นทแยงมุมจากซ้ายบนลงมาขวาล่าง เราเรียกเส้นทแยงมุมในแนวนี้ว่า เส้นทแยงมุมหลัก (main diagonal) การคูณเมตริกซ์ บทนิยาม ให้  และ k เป็นจำนวนจริงใด ๆ จะได้ว่า สรุปบลักษณะการคูณจำนวนจริงกับเมทริกซ์ ให้ a , b เป็นจำนวนจริง และ A , B เป็นเมทริกซ์ที่มีมิติ 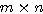 1. aA = Aa 2. (ab)A = a(bA) = b(aA) 3. a(A + B) = aA + aB 4. (a +b)A = aA + aB เมตริกซ์              เป็นคำที่ยากที่จะนิยามความหมายให้ชัดเจน แต่เป็นที่ทราบโดยทั่วกันว่าเมตริกซ์มี ลักษณะเป็นชุดข้อมูลที่มีการเรียงกันเป็นแนวแถว (Row) และแนวหลัก (Column) ดังตัวอย่าง เมตริกซ์ A, B และ Cดังนี้ A =       5 6 7 2 3 4 , B =       3 4 1 2 , C = [1 5 6] โดยทั่วไปแล้วจะใช้ตัวพิมพ์ใหญ่ (A, B, C,…) แทนเมตริกซ์ส่วนสมาชิกของเมตริกซ์จะใช้ แทนด้วยตัวพิมพ์เล็กพร้อมทั้งระบุตำแหน่งของสมาชิกว่าอยู่ต าแหน่งใดของเมตริกซ์ตัวอย่างเช่น a12 จะแทนสมาชิกในแถวที่ 1 หลักที่ 2 ของ เมตริกซ์ A และ b22 จะแทน สมาชิก ในแถวที่  2 หลักที่  2 ของเมตริกซ์ B เป็นต้น ในคณิตศาสตร์ เมทริกซ์ หรือ เมตริกซ์ (อังกฤษ: matrix) คือตารางสี่เหลี่ยมที่แต่ละช่องบรรจุจำนวนหรือโครงสร้างทางคณิตศาสตร์ที่สามารถนำมาบวกและคูณกับตัวเลขได้ เราสามารถใช้เมทริกซ์แทนระบบสมการเชิงเส้น การแปลงเชิงเส้น และใช้เก็บข้อมูลที่ขึ้นกับตัวแปรต้นสองตัว เราสามารถบวก คูณ และแยกเมทริกซ์ออกเป็นผลคูณของเมทริกซ์ได้หลายรูปแบบ เมทริกซ์เป็นแนวความคิดที่มีความสำคัญยิ่งของพีชคณิตเชิงเส้น โดยทฤษฎีเมตริกซ์เป็นสาขาหนึ่งของพีชคณิตเชิงเส้นที่เน้นการศึกษาเมตริกซ์ ชนิดของเมตริกซ์               1. เมทริกซ์จัตุรัส              2. เมทริกซ์เอกลักษณ์              3. เมทริกซ์ศูนย์              4. เมทริกซ์ทแยงมุม              5. เมทริกซ์สเกลาร์              6. เมทริกซ์สลับเปลี่ยน   1. เมทริกซ์จัตุรัส เป็นเมทริกซ์ที่มีจำนวนแถวและจำนวนสดมภ์เท่ากัน เช่น         A = เป็นเมทริกซ์จัตุรัสมิติ 2x2 ที่มีจำนวนแถว 2 แถวและจำนวนสดมภ์ 2 สดมภ์                   B =  เป็นเมทริกซ์จัตุรัสมิติ 3x3 ที่มีจำนวนแถว 3 แถวและจำนวนสดมภ์ 3 สดมภ์            2. เมทริกซ์เอกลักษณ์ เป็นเมทริกซ์จัตุรัสที่สมาชิกในตำแหน่งแถวเท่ากับตำแหน่งสดมภ์จะมีสมาชิกมีค่าเป็น 1 และในทางกลับกันสมาชิก ในตำแหน่งแถวไม่เท่ากับตำแหน่งสดมภ์ จะมีสมาชิกมีค่าเป็น 0 เป็นตัวอย่างของเมทริกซ์เอกลักษณ์มิติ 2x2              เป็นเมทริกซ์เอกลักษณ์มิติ 2x2  ตำแหน่งแถวเท่ากับตำแหน่งสดมภ์ มีสมาชิกในตำแหน่งแถวที่ 1 สดมภ์ที่ 1 และสมาชิกที่อยู่ตำแหน่งแถวที่ 2 สดมภ์ที่ 2 มีค่าสมาชิกเป็น  1  ตำแหน่งแถวไม่เท่ากับตำแหน่งสดมภ์  สมาชิกที่อยู่ ในตำแหน่งแถวที่ 1 สดมภ์ที่ 2 และ สมาชิกที่อยู่ในตำแหน่งแถวที่ 2  สดมภ์ที่ 1 มีค่าเป็น  0   แสดงเมทริกซ์เอกลักษณ์มิติ 3x3 B =              B เป็นเมทริกซ์เอกลักษณ์มิติ 3x3  ที่มีสมาชิกที่อยู่ในตำแหน่งแถวที่ 1 สดมภ์ที่ 1, ตำแหน่งแถวที่ 2 สดมภ์ที่ 2 และ ตำแหน่งแถวที่ 3 สดมภ์ที่ 3 เป็น 1 เพราะตำแหน่งแถวเท่ากับตำแหน่งสดมภ์  ที่เหลือของสมาชิกมีค่าเป็น 0  เพราะตำแหน่งแถวไม่เท่ากับตำแหน่งสดมภ์                ดังนั้นสามารถเขียนสมาชิกของเมทริกซ์เอกลักษณ์เป็นรูปทั่วไปได้ดังนี้ aij =      , i เท่ากับ j      , i ไม่เท่ากับ j                 เมื่อ  i    เป็นตำแหน่งแถว และ  j เป็นตำแหน่งสดมภ์                       aij   เป็นสมาชิกของตำแหน่งแถวที่ i  และตำแหน่งสดมภ์ที่ j                3. เมทริกซ์ศูนย์  เป็นเมทริกซ์ที่มีสมาชิกทุกตัวเป็นศูนย์                             แสดงเมทริกซ์ที่มีสมาชิกเป็นศูนย์ทั้งที่เป็นไม่ใช่เมทริกซ์จัตุรัสและเมทริกซ์จัตุรัส                                                               จะเห็นว่าเมทริกซ์ทางซ้าย  ตอนกลาง  เป็นเมทริกซ์ที่ไม่ใช่จัตุรัส แต่ที่สมาชิกเป็นศูนย์  ส่วนเมทริกซ์ขวาสุด  เป็นเมทริกซ์จัตุรัส ที่มีสมาชิกทุกตัวเป็นศูนย์                 4. เมทริกซ์ทแยงมุม เป็นเมทริกซ์จัตุรัสที่มีสมาชิกที่อยู่เหนือและใต้ทแยงมุมเป็นศูนย์                              แสดงเมทริกซ์ทแยงมุมที่มีมิติ 2x2, 3x3                                                                     ข้อสังเกต สมาชิกที่อยู่ในแนวทแยงมุมมีค่าไม่เท่ากัน แต่สมาชิกที่อยู่เหนือหรือใต้เส้นทแยงมุมเป็นศูนย์                  5. เมทริกซ์สเกลาร์  เป็นเมทริกซ์จัตุรัส ที่มีสมาชิกที่อยู่ในแนวทแยงมุมเท่ากัน และสมาชิกที่อยู่เหนือ, ใต้ทแยงมุมเป็นศูนย์                                     แสดงเมทริกซ์สเกลาร์มิติ 2x2, 3x3                                                            จะเห็นว่าสมาชิกในแนวทแยงมีค่าเท่ากันแต่สมาชิกที่อยู่เหนือทแยงมุมและใต้ทแยงมุมเป็นศูนย์            6. เมทริกซ์สลับเปลี่ยน เป็นเมทริกซ์ที่มีสมาชิกที่อยู่ในแนวแถวมาจากสมาชิกในแนวสดมภ์ห รือสมาชิกที่อแนวสมาชิกที่อยู่ในแนวสดมภ์ เป็นสมาชิกในแนวแถว ซึ่งมีสัญลักษณ์ เป็น AT หรือ At                              ให้ A เป็นเมทริกซ์มิติ 2x2 และ B เป็นเมทริกซ์มิติ 2x3 A = , B =                        2x2                          2x3 การดำเนินการเมทริกซ์            ดีเทอร์มิแนนต์     ในสาขาพีชคณิต ดีเทอร์มิแนนต์ (อังกฤษ: determinant) คือฟังก์ชันหนึ่งที่ให้ผลลัพธ์เป็นปริมาณสเกลาร์ ซึ่งขึ้นอยู่กับค่าของ n ในมิติ n×n ของเมทริกซ์จัตุรัส A ส่วนความหมายทางเรขาคณิตเบื้องต้น ดีเทอร์มิแนนต์คือตัวประกอบ มาตราส่วน (scalefactor) ของปริมาตร เมื่อ A ถูกใช้เป็นการแปลงเชิงเส้น ดีเทอร์มิแนนต์ถูกใช้ประโยชน์ในเรื่องพีชคณิตเชิงหลายเส้น (multilinearalgebra) และแคลคูลัส ซึ่งใช้สำหรับกฎการแทนที่ (substitutionrule)    ในตัวแปรบางกลุ่มสำหรับจำนวนเต็มบวก n ที่กำหนดขึ้น  ฟังก์ชันดีเทอร์มิแนนต์จะมีเพียงหนึ่งเดียวบนเมทริกซ์มิติ n×n เหนือริงสลับที่ใดๆ (commutative ring) โดยเฉพาะเมื่อฟังก์ชันนี้นิยามไว้บนริงสลับที่ที่เป็นฟีลด์ของ จำนวนจริง หรือจำนวนเชิงซ้อน                  อินเวอร์สการคูณเมทริกซ์ (Matrix Inverse)                          ให้ A เป็นเมทริกซ์มิติ n×n  ถ้า B เป็นเมทริกซ์มิติ n×n และมีสมบัติว่า                                                         AB=BA=In            เมื่อ In เป็นเมทริกซ์เอกลักษณ์แล้วเราเรียก B ว่าเป็นเมทริกซ์อินเวอร์สของ A และเขียน B แทนด้วย A−1                          อินเวอร์สของเมทริกซ์ขนาด 2×2                                                     ให้ A=[acbd] และ detA=ad−cb≠0 แล้ว                                             A−1=1ad−cb[d−c−ba]       ตัวอย่างการหาอินเวอร์สของเมทริกซ์ขนาด 2×2                                      ให้ A=[1324]                           เนื่องจาก detA=1⋅4−2⋅3=−2≠0 ดังนั้น A−1  หาค่าได้คือ                                              A−1==1−2[4−3−21][−2321−12] การแก้ระบบสมการเชิงเส้นโดยใช้เมตริกซ์             การแก้ระบบสมการเชิงเส้นโดยวิธีนี้จะใช้ได้สะดวกที่สุดเมื่อระบบสมการเชิงเส้นมี 2 ตัวแปรแต่เมื่อระบบสมการเชิงเส้นของเรามีตัวแปรมากกว่า 3ตัวแปร ในบางครั้งการแก้ระบบสมการโดยวิธีนี้ค่อนข้างจะยุ่งยากจึงไม่เป็นที่นิยม การแก้ระบบสมการเชิงเส้น 2 ตัวแปรโดยการกำจัดตัวแปรให้ระบบสมการ                                x−2y2x+1y==3⋯(1)1⋯(2)                  นำ 2×(2)             จะได้    4x+2y=2⋯(3)                 นำสมการ (1)+(3)    จะได้    5x=5                 ดังนั้นเราได้ x=1                 เมื่อนำค่า x=1 ไปแทนในสมการ (1) จะได้  y=−1                 ดังนั้น x=1,y=−1